Kryptologi til forskningens døgn
Table of Contents
Halli halløj, og velkommen til kryptologiens verden! Her skal I prøve kræfter med et par eksempler på kryptologi. De er delt op efter emne, så hvis man går død i et af emnerne kan man gå prøve at gå videre til det næste.
I alle opgaverne kan man finde hints og løsninger, som dukker frem hvis man klikker på dem (tablet/telefon) eller holder musen over dem (computer).
God fornøjelse, og hold jer endelig ikke tilbage fra at stille os spørgsmål!
1. Substitution
Et klassisk eksempel på en kryptering er det her:
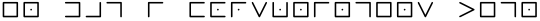
Kender du kryptosystemet? Det bliver ofte kaldet juniorkoden eller frimurekoden. Ellers kan du se den simple nøgle man bruger til at kryptere og dekryptere beskeder herunder:

Opgave 1
Prøv at dekryptere beskeden ved at bruge nøglen.
Løsning
EN DAG I FORSKNINGENS TEGN
Problem
Det her system er nemt at bryde, selv hvis man ikke har koden. Hvert bogstav bliver altid oversat til det samme tegn. Selv hvis man finder på sit eget system, så kan man faktisk nemt bryde den her slags kryptering, som i vil finde ud af i næste opgave.
2. Frekvensanalyse
Et af de klassiske redskaber som man kan bruge til at bryder koder som den ovenstående, er frekvensanalyse. Dette virker ved at observerer at der er forskel på hvor ofte forskellige bogstaver bliver brugt, så hvis man på forhånd ved hvor ofte forskellige bogstaver bliver brugt i et sprog kan man ofte gætte hvilket symbol der svare til hvilket bogstav, ved at tælle hvor mange gange hvert symbol forekommer i en lang besked.
På engelsk er frekvensen af forskellige bogstaver følgende.
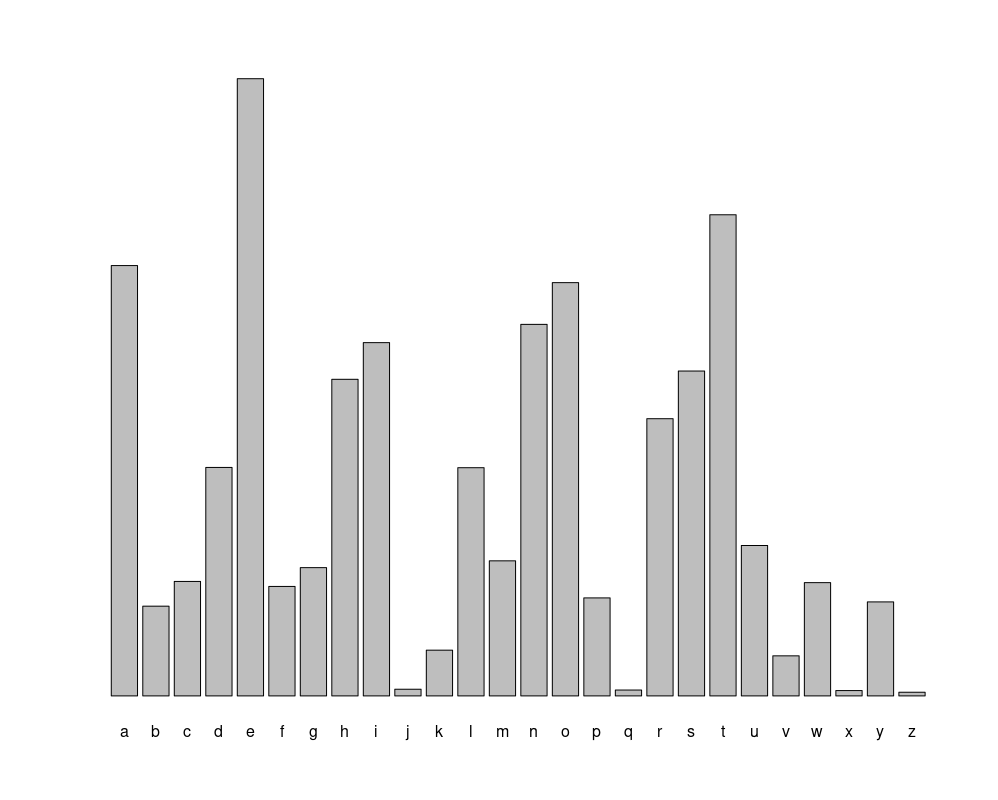
Opgave 2
I har opsnappet en lang krypteret besked fra England, og vil gerne finde ud af hvad den siger. Beskeden starter
\begin{align} \text{mit mtlm ltektm ol miam mitkt ol fg ltektm ass}&\notag\\ \text{gy miol tyygkm ial zttf ygk fgmiofu}&... \end{align}Det ligner jo volapyk! Men et gæt kunne være at de har brugt en alfabets-substitution, hvor man erstatter hvert bogstav med et andet bogstav.
I har analyseret hvor mange gange hvert bogstav bliver brugt i beskeden, og er kommet frem til følgende fordeling.
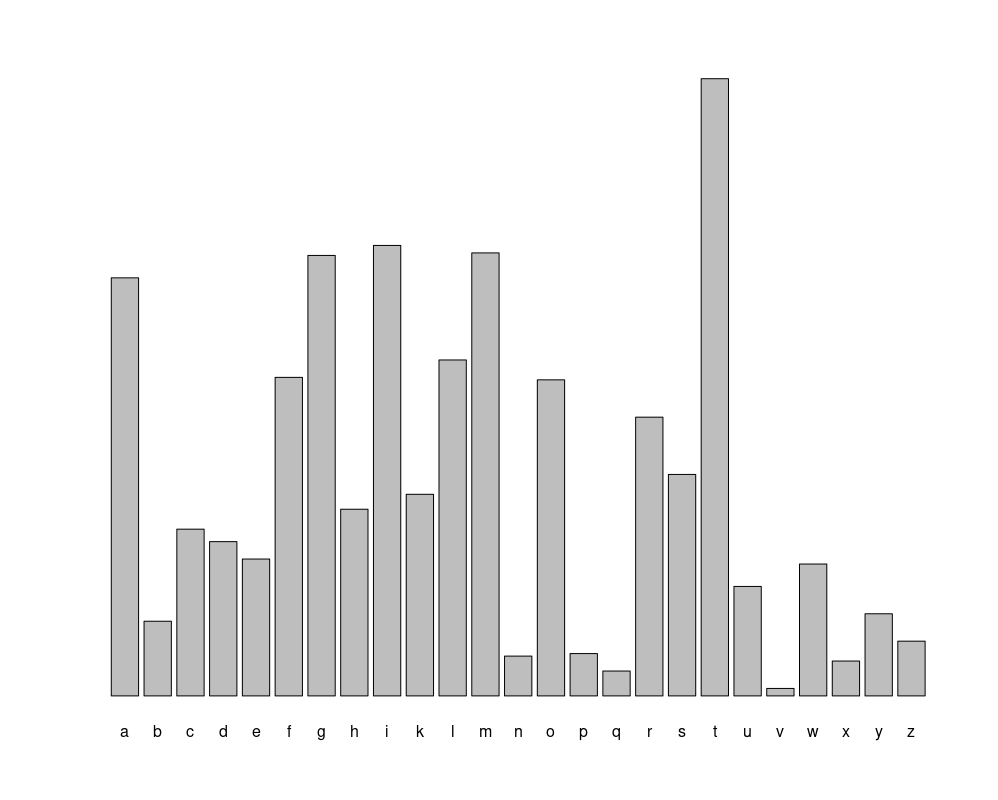
De første 15 symboler i beskeden er
\begin{align} \text{m}\quad{}\text{i}\quad{}\text{t}\quad{}\text{ }\quad{}\text{m}\quad{}\text{t}\quad{}\text{l}\quad{}\text{m}\quad{}\text{ } \quad{}\text{l}\quad{}\text{t}\quad{}\text{e}\quad{}\text{k}\quad{}\text{t}\quad{}\text{m} \end{align}Find ud af hvad de første 15 symboler af beskeden siger.
Hint
Start med at se på det mest brugte bogstav (t). Det må næsten være et e. Se dernæst på det første bogstav i det første ord (m). Det høre til de bogstaver som der er 2. flest af (sammen med a,g, og i), så det må næsten svare til a, n, i, eller t. Passer nogen af dem med et 3 bogstavs ord der slutter med e, og et fire bogstavs ord der starter og slutter med dette bogstav, og har et e som andet bogstav?
Når du har fundet ud af ovenstående, så se om ikke du kan gætte hvad første og andet ord må være. Brug dette til at gætte hvad 3. ord er.
Løsning
Beskedens start er
\begin{align} \text{the test secret} \end{align}3. En helt sikker kode
Ovenfor har i set kryptosystemer som er nemme at bryde. Problemet med systemerne er at vi bruger den samme nøgle til at kryptere hele beskeden. Hvad hvis nu vi bruger en ny nøgle til hvert eneste symbol? Så ville man potentielt kunne få en hvilken som helst besked ud af en kryptering, bare ved at vælge den rigtige nøgle! På den måde får vi perfekt sikkerhed! Et system der fungere på den her måde bliver kaldt et one-time-pad.
Ideen er at vi giver hvert bogstav en tal værdi, og så kan vi kan kryptere et bogstav ved at bruge et andet bogstav som nøgle, på den måde at vi lægger deres talværdi sammen, så vi får et tredje bogstav, som vi så bruger som vores krypterede besked.
Vi giver hvert bogstav følgende værdi:
\begin{align} \begin{matrix} \text{a}: & 1 &\quad& \text{b}: & 2 &\quad& \text{c}: & 3 &\quad& \text{d}: & 4 &\quad& \text{e}: & 5\\ \text{f}: & 6 &\quad& \text{g}: & 7 &\quad& \text{h}: & 8 &\quad& \text{i}: & 9 &\quad& \text{j}: & 10\\ \text{k}: & 11 &\quad& \text{l}: & 12 &\quad& \text{m}: & 13 &\quad& \text{n}: & 14 &\quad& \text{o}: & 15\\ \text{p}: & 16 &\quad& \text{q}: & 17 &\quad& \text{r}: & 18 &\quad& \text{s}: & 19 &\quad& \text{t}: & 20\\ \text{u}: & 21 &\quad& \text{v}: & 22 &\quad& \text{w}: & 23 &\quad& \text{x}: & 24 &\quad& \text{y}: & 25\\ \text{z}: & 26 &\quad& \text{æ}: & 27 &\quad& \text{ø}: & 28 &\quad& \text{å}: & 29 & & & \end{matrix} \end{align}Hvis vi nu vil kryptere et s (19) med et k (11) som nøgle får vi
\begin{align} 19 + 11 = 30 \equiv 1 \pmod{29}, \end{align}så vi bruger a som krypteringen af s. Hvis vi kender krypteringen og nøglen kan vi dekryptere beskeden ved at trække nøglen fra:
\begin{align} 1 - 11 = -10 \equiv 19 \pmod{29}. \end{align}Opgave 3
I har aftalt med jeres kammerater at i bruger nøglen
\begin{align} \text{m}\quad\text{a}\quad\text{t}\quad\text{h}. \end{align}De har sendt jer en krypteret besked,
\begin{align} \text{q}\quad\text{å}\quad\text{æ}\quad\text{v}. \end{align}Hvad er beskeden de har krypteret?
Løsning
Jeres kammerater har sendt jer beskeden
\begin{align} \text{d}\quad\text{ø}\quad\text{g}\quad\text{n}. \end{align}Opgave 4: Sikkerhed
For at se at den her måde at kryptere på er fuldstændig sikker, kan i prøve at se om i kan finde ud af hvilken nøgle man skulle have brugt for at det ovenfor havde været en kryptering af beskeden
\begin{align} \text{k}\quad\text{o}\quad\text{d}\quad\text{e}. \end{align}Løsning
For at finde ud af hvilken nøgle man skal bruge for at få et bestemt bogstav kan vi lægge det krypterede bogstav til bogstavet vi gerne vil have krypteringen til at give. F.eks. vil vi gerne have q (17) til at dekryptere til k (11), så vi får
\begin{align} 17 - 11 = 6 \pmod{29}, \end{align}så vi bruger f som det første bogstav i den alternative nøgle. Gentager vi det samme for de andre tre bogstaver får vi at den alternative nøgle er
\begin{align} \text{f}\quad\text{n}\quad\text{w}\quad\text{q}. \end{align}Problemer og løsninger (ikke nødvendigt at læse)
Dette system kræver at vores nøgle er ligeså lang som den besked vi sender, for hvis vi begynder at genbruge vores nøgle så ender vi (hvis vi sender nok tekst) med et kryptosystem som man kan bruge en lidt mere avanceret form for frekvensanalyse på. Udover længden af vores nøgle har vi også et problem med hvordan vi skal dele nøglen i første omgang. Hvis vi sender beskeder til en vi kender i virkeligheden kan vi måske bare udveksle vores nøgler når vi er sammen i virkeligheden, men hvad hvis det er en vi kun kender online - der virker det til at være lige så svært som at sende en hemmelig besked i første omgang.
Den måde som vi løser disse problemer på er ved hjælp af to forskellige værktøjer:
- Asymmetrisk kryptering bruger vi til at udveksle korte nøgler gennem åbne kanaler, sådan at de forbliver sikre. Helt kort fungere et asymmetrisk kryptosystem ved at man har en offentlige nøgle og en hemmelig nøgle. Med den offentlige nøgle kan kryptere beskeder som så kan dekrypteres med den hemmelige nøgle, men ikke med den offentlige nøgle. Det betyder at man kan dele sin offentlige nøgle offentligt, andre kan så kryptere den besked de vil dele med os med den offentlige nøgle, sende krypteringen af den til os, og vi kan så finde beskeden ved at bruge vores hemmelige nøgle. Problemet med asymmetrisk kryptering er at det oftest er langsomt at bruge.
- Symmetrisk kryptering har vi allerede set tre eksempler på; både juniorkoden, alfabets-substitution, og one-time-pad er symmetriske krypteringer. Her har begge parter den samme nøgle, som de både kan bruge til at kryptere og dekryptere. Udfordringen for moderne symmetriske kryptosystemer er hvordan man kan bruge en kort nøgle til at få noget der stadig er sikkert. En måde man kan gøre dette på er ved at bruge en algoritme hvor man tager en kort nøgle og får noget langt output, som virker fuldstændig tilfældigt, og så bruge samme fremgangsmåde som i one-time-pad. Problemet med symmetrisk kryptering er som beskrevet ovenfor: hvordan udveksler vi koden i første omgang?
Løsningen er så at kombinere asymmetrisk og symmetrisk kryptering! Vi bruger et asymmetrisk kryptosystem til at udveksle en kort nøgle, som vi så kan bruge i et symmetrisk kryptosystem til at udveksle en længere besked. Dette er præcis den måde som hele internettets sikkerhed fungere på!
4. Hemmelighedsdeling
Et andet emne som kryptografer arbejder med er hemmelighedsdeling. Kort fortalt, så handler hemmelighedsdeling om hvordan man kan dele en hemmelighed mellem flere personer, sådan at de kun kan finde hemmeligheden ved at arbejde sammen.
Et eksempel kunne være at chefen sender Alice og Bob ud for at købe snacks med hans kort. Men chefen ved at hvis Alice har koden så køber hun ikke andet end saltlakrids, og hvis Bob har koden så køber han ikke andet end selleri. Derfor vil han gerne dele koden mellem dem, sådan så de kun kan finde koden ved at arbejde sammen, så han får en god blanding af snacks.
For at gøre dette kan chefen tegne en tilfældig streg som skære y-aksen i koden, og så give Alice og Bob et punkt hver.
Opgave 5
Alice og Bob har fundet en god blanding af sunde snacks og lakrids, og vil derfor gerne arbejde sammen om at finde koden så chefen kan få lov til at betale for dem. Alice har fået punktet \((1,2459)\) og Bob har fået punktet \((2,3581)\). Hvad er koden?
Hint
Givet to punkter \((x_1,y_1)\) og \((x_2,y_2)\) kan man finde hældningen af den unikke linje der går gennem dem med formlen
\begin{align} a = \frac{y_2-y_1}{x_2-x_1}, \end{align}og når man har fundet hældningen kan man finde skæringen af med y-aksen ved
\begin{align} b = y_1 - a \cdot x_1, \end{align}da
\begin{align} y_1 = a \cdot x_{1} + b \Leftrightarrow b = y_1 - a \cdot x_1. \end{align}Løsning
Fylder vi ind i ligningerne får vi at
\begin{align} a = \frac{3581-2459}{2-1} = 1122, \end{align}så koden må være
\begin{align} b = 2459 - 1122 \cdot 1 =1337. \end{align}Opgave 6: Sikkerhed
For at overbevise os selv om at vores system er sikkert, og at Alice altså ikke kan finde koden uden Bob, kan vi vise at hvis Alice ikke kender Bobs del af hemmeligheden, så kunne den ligeså godt være enhver anden hemmelighed.
Gør dette ved at se på nedenstående eksempel, og find ud af hvad Bobs hemmelighed kan være for at koden er \(1\) og at koden er \(7\).
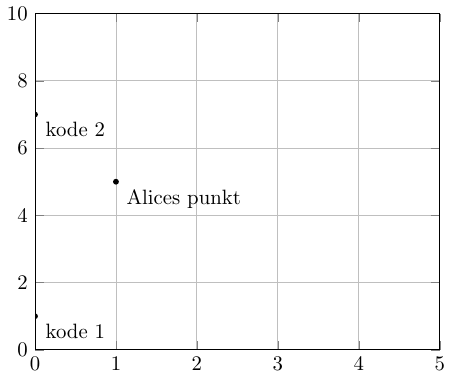
Overvej om man kan gøre det samme for alle andre koder og for Bob. Har Alice og Bob mulighed for at lære noget som helst uden at arbejde sammen?
Løsning
Hvis Bob har punktet \((2,9)\) passer det med kode 1, og hvis Bob har punktet \((2,3)\) passer det med kode 2.
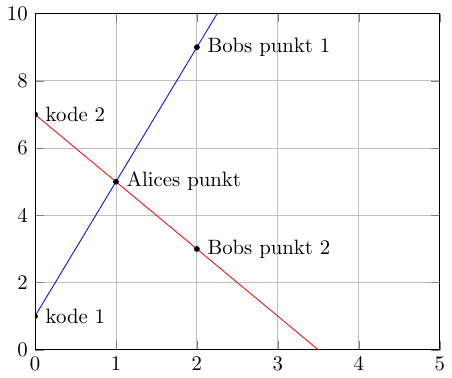
Det samme kan gøres for alle andre koder og for Bob, så Alice og Bob kan altså ikke lære noget uden at arbejde sammen.
Opgave 7
Chefen ved godt at Alice og Bob måske kan blive enige. Han sender derfor også Charles med ud, og vil gerne have at det er nok hvis \(2\) af de \(3\) er enige. Hvad skal han gøre for at få hans hammemelighedsdelingssystem til at virke i denne situation?
Løsning
Chefen kan bare give Charles punktet med x-koordinatet \(3\). Så kan to parter stadig bruge formlen fra opgave 5, og argumentet for at systemet er sikkert holder stadig.
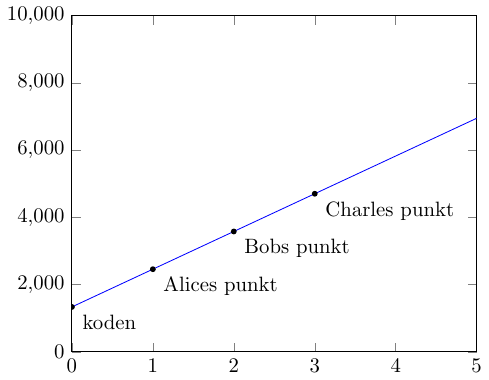
Opgave 8 (udfordrende)
Overvej hvad chefen kan gøre hvis chefen vil have at både Alice, Bob, og Charles er enige? Hvad hvis chefen sender \(k\) medarbejdere i byen, som alle skal være enige?
Hint/løsning
Hvis chefen gerne vil have at alle tre er enige kan han give dem hvert et punkt på et 2-grads polynomie, som skære y-aksen i koden.
Generelt er det tilfældet at hvis man kender \(n+1\) punkter kan man finde det unikke \(n\)'te grads polynomie der går gennem alle \(n\) punkter med formlen
\begin{align} p(x) = \sum_{j=1}^{n+1}y_j \cdot L_j(x), \end{align}hvor
\begin{align} L_j(x) = \prod_{\stackrel{{i=1}}{i \ne j}}\frac{x-x_{i}}{x_j-x_{i}}. \end{align}Hvis man derimod kun kender \(n\) punkter er der uendeligt mange \(n\)'te grads polynomier der går gennem disse punkter.
Chefen kan derfor dele koden ved at finde et \(k-1\)'ne grads polynomie der skære y-aksen i koden, og så give hvert af medarbejderne et punkt \((x_1,y_1),\ldots,(x_k,y_k)\). Så kan de - hvis de arbejder sammen - finde koden ved at bestemme \(p(0)\).
\begin{align} p(0) = \sum_{j=1}^{n+1}y_j \cdot L_j(0) = \sum_{j=1}^{n+1}y_j \cdot \prod_{\stackrel{{i=1}}{i \ne j}}\frac{-x_{i}}{x_j-x_{i}}. \end{align}Opgave 9: Mere opgave 8
Herunder ses et eksempel med \(k=4\), hvor Alice har fået \((1,5336)\), Bob har fået \((2,5777)\), Charles har fået \((3,5324)\), og David har fået \((4,6641)\).
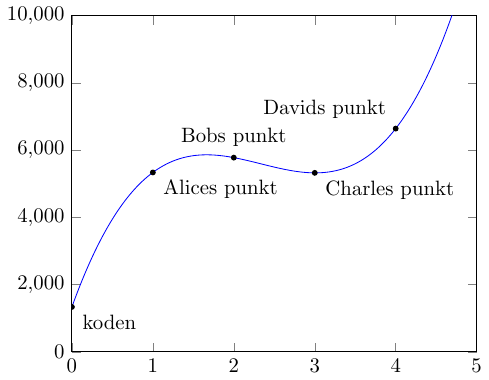
Kan du finde ud af hvad koden er - og hvad polynomiet er?
Hint
Se på hint/løsning til opgave 8.
Test
Når du har fundet ud af hvad koden er så indtast den her: